[39회차 수업내용] 250711
1. 하노이 타워의 재귀
2. 순차 탐색
3. 이진탐색
4. 이진탐색트리
5. 깊이 우선 탐색
6. 너비 우선 탐색
1. 하노이 타워의 재귀
public void HanoiAnswer()
{
// 하노이 탑 문제를 시작하는 함수
// n = hanoiLevel 만큼의 원판을 0번 기둥에서 2번 기둥으로 옮긴다
// 1번 기둥은 임시로 사용
HanoiRoutine((int)hanoiLevel, 0, 1, 2);
}
private void HanoiRoutine(int n, int from, int temp, int to)
{
// 원판이 1개일 경우
if (n == 1)
Debug.Log($"{n}번 도넛을 {from}에서 {to}로 이동"); // 직접 이동 출력
else
{
// n-1개의 원판을 from에서 temp로 옮김 (to는 임시 기둥)
HanoiRoutine(n - 1, from, to, temp);
// 가장 큰 원판(n번)을 from에서 to로 이동 출력
Debug.Log($"{n}번 도넛을 {from}에서 {to}로 이동");
// n-1개의 원판을 temp에서 to로 옮김 (from은 임시 기둥)
HanoiRoutine(n - 1, temp, from, to);
}
}
2. 순차 탐색 (Linear Search) → O(n)
- 배열의 첫 원소부터 차례로 하나씩 비교하면서 원하는 값(target)을 찾는 탐색 방법.
- 최악의 경우 배열 끝까지 확인하므로 시간 복잡도는 O(n).
- 데이터가 정렬되어 있지 않거나, 작은 배열에서 쉽게 사용.
public class LinearSearch : MonoBehaviour
{
// 탐색할 배열 (1부터 10까지 순서대로 저장)
private int[] array = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
// 찾고자 하는 값
public int target = 7;
void Start()
{
// 배열에서 target 값을 순차 탐색하는 함수 호출
LSearch(array, target);
}
// 순차 탐색 함수
// arr: 탐색할 배열, t: 찾고자 하는 값
private void LSearch(int[] arr, int t)
{
// 배열 처음부터 끝까지 한 칸씩 차례대로 확인
for (int i = 0; i < arr.Length; i++)
{
// 현재 원소가 찾는 값과 같으면 위치 출력
if (arr[i] == t)
{
Debug.Log($"{t}은 {i}번째에 있습니다.");
// 찾았으니 탐색 종료해도 됨 (필요시 break 추가 가능)
// break;
}
}
}
}
3. 이진 탐색 (Binary Search) → O(logn)
- 정렬된 배열에서 원하는 값을 찾는 효율적인 탐색 알고리즘.
- 배열의 중간 값을 기준으로 찾는 값과 비교해 크면 왼쪽 절반, 작으면 오른쪽 절반을 탐색 범위에서 제거하며 검색 범위를 좁혀나감.
- 매번 탐색 범위를 반으로 줄이므로 시간 복잡도는 O(log n)으로 매우 빠름.
public class BinarySearch : MonoBehaviour
{
// 이진 탐색은 **정렬된 배열**에서만 사용 가능
private int[] array = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
private int target = 7; // 찾고자 하는 값
void Start()
{
// 이진 탐색 실행, 결과는 target이 있는 인덱스 (없으면 -1)
int result = BSearch();
Debug.Log($"{target}은 {result}번째에 있습니다.");
}
// 이진 탐색 함수
private int BSearch()
{
int left = 0; // 탐색 범위의 시작 인덱스
int right = array.Length - 1; // 탐색 범위의 끝 인덱스
// left가 right보다 작거나 같을 때까지 반복
while (left <= right)
{
int mid = (left + right) / 2; // 중간 인덱스 계산
// 중간 값이 찾는 값이면 인덱스 반환
if (array[mid] == target)
return mid;
// 중간 값이 target보다 작으면 왼쪽 절반 버리고 오른쪽 탐색
else if (array[mid] < target)
left = mid + 1;
// 중간 값이 target보다 크면 오른쪽 절반 버리고 왼쪽 탐색
else
right = mid - 1;
}
// 탐색 실패 시 -1 반환
return -1;
}
}
4. 이진 탐색 트리 (BST : Binary Search Tree) → O(logn)
: 이진 탐색 트리는 데이터를 효율적으로 저장하고 검색, 삽입, 삭제할 수 있도록 설계된 트리(Tree)
- 각 노드는 최대 두 개의 자식 노드를 가질 수 있음
- 왼쪽 자식: 어떤 노드의 왼쪽 서브트리(왼쪽 자식과 그 자손들)에 있는 모든 값은 현재 노드의 값보다 작음
- 오른쪽 자식: 어떤 노드의 오른쪽 서브트리(오른쪽 자식과 그 자손들)에 있는 모든 값은 현재 노드의 값보다 큼
- 중복 값: 일반적으로 중복 값은 허용하지 않거나, 오른쪽 서브트리에 저장
- 루트 노드: 트리의 가장 꼭대기에 있는 노드
- 삽입 및 삭제 용이: 데이터를 추가하거나 제거하기도 비교적 쉬움
- 정렬된 데이터 유지: 중위 순회(InOrder traversal)를 하면 항상 정렬된 순서로 데이터를 얻을 수 있음
using System;
using UnityEngine;
// 이진 탐색 트리(Binary Search Tree)를 구현하는 클래스
public class BinarySearchTree : MonoBehaviour
{
// 트리의 노드 클래스
public class TreeNode
{
public TreeNode left; // 왼쪽 자식 노드 (작은 값)
public TreeNode right; // 오른쪽 자식 노드 (큰 값)
public int value; // 노드에 저장된 값
public TreeNode(int value) //
{
this.value = value; // 노드를 만들 때 값을 초기화
}
}
private TreeNode root; // 트리의 루트 노드
private int[] array = { 8, 3, 10, 1, 6, 14, 4, 7, 13 }; // 삽입할 값 배열
private string result; // 순회 결과를 저장할 문자열
void Start()
{
// 배열의 모든 값을 이진 탐색 트리에 삽입
foreach (var v in array)
root = Insert(root, v);
// 전위 순회 (루트 -> 왼쪽 -> 오른쪽)
PreOrder(root);
Debug.Log($"PreOrder : {result.TrimEnd(',')}");
// 결과 초기화 후 중위 순회 (왼쪽 -> 루트 -> 오른쪽)
result = string.Empty;
InOrder(root);
Debug.Log($"InOrder : {result.TrimEnd(',')}");
// 결과 초기화 후 후위 순회 (왼쪽 -> 오른쪽 -> 루트)
result = string.Empty;
PostOrder(root);
Debug.Log($"PostOrder : {result.TrimEnd(',')}");
}
// 트리에 값을 삽입하는 함수 (재귀)
private TreeNode Insert(TreeNode node, int v)
{
// 현재 노드가 null이면 새로운 노드 생성 후 반환
if (node == null)
return new TreeNode(v); // 첫 노드 = 루트 에 첫 값을 넣기
// 삽입할 값이 현재 노드 값보다 작으면 왼쪽 서브트리에 삽입
if (v < node.value)
node.left = Insert(node.left, v);
else // 크거나 같으면 오른쪽 서브트리에 삽입
node.right = Insert(node.right, v);
return node; // 삽입 후 현재 노드 반환
}
// 전위 순회: 루트 -> 왼쪽 -> 오른쪽
private void PreOrder(TreeNode node)
{
if (node == null)
return;
// 현재 방문한 노드의 값을 result라는 문자열 변수에 계속해서 추가
result += $"{node.value}, ";
PreOrder(node.left);
PreOrder(node.right);
}
// 중위 순회: 왼쪽 -> 루트 -> 오른쪽 (이진 탐색 트리의 정렬된 순서 출력)
private void InOrder(TreeNode node)
{
if (node == null)
return;
InOrder(node.left);
result += $"{node.value}, ";
InOrder(node.right);
}
// 후위 순회: 왼쪽 -> 오른쪽 -> 루트
private void PostOrder(TreeNode node)
{
if (node == null)
return;
PostOrder(node.left);
PostOrder(node.right);
result += $"{node.value}, ";
}
}
4.1 트리 순회
:트리의 모든 노드를 방문하는 방법을 의미]
- 전위 순회 (PreOrder): 루트 방문 → 왼쪽 서브트리 → 오른쪽 서브트리 // 트리 구조를 복사하거나 표현할 때 유용
- 중위 순회 (InOrder): 왼쪽 서브트리 → 루트 → 오른쪽 서브트리 // BST에서 오름차순 정렬된 결과를 얻음
- 후위 순회 (PostOrder): 왼쪽 서브트리 → 오른쪽 서브트리 → 루트 // 트리 삭제나 후처리 작업 시 사용
array = { 8, 3, 10, 1, 6, 14, 4, 7, 13 }
//트리
8
/ \
3 10
/ \ \
1 6 14
/ \ /
4 7 13
//순회 결과
PreOrder: 8, 3, 1, 6, 4, 7, 10, 14, 13
InOrder: 1, 3, 4, 6, 7, 8, 10, 13, 14 (정렬된 순서!)
PostOrder: 1, 4, 7, 6, 3, 13, 14, 10, 8*노드 = 데이터 하나와 그 데이터와 연결된 다른 노드들의 집합(구조)
*트리 <-> 그래프
| 트리 | 그래프 | |
| 구조 | 계층적 구조 (부모-자식 관계) | 네트워크 구조 (복잡한 연결 가능) |
| 순환(사이클) | 없음 (사이클 X) | 있을 수도 있고, 없을 수도 있음 |
| 연결성 | 모든 노드가 연결되어 있어야 함 | 연결되지 않은 노드도 존재할 수 있음 |
| 방향성 | 일반적으로 방향 있음 (부모 → 자식) | 방향 그래프(방향 有), 무방향 그래프(방향 無) 모두 가능 |
| 루트 노드 | 반드시 하나의 루트 노드 존재 | 루트 없음 |
| 간선 개수 | 노드 수 - 1개 | 제한 없음 |
| 예시 | 가계도, 폴더 구조, 조직도 | 도로망, 소셜 네트워크, 지도 |
5. 깊이 우선 탐색 (DFS : Depth First Search)
- 노드 수가 N개일 때: O(N)
- 트리나 그래프에서 한 방향으로 계속 깊이 내려가며 탐색하는 방법
- 더 이상 내려갈 곳이 없으면 다시 돌아와서(백트래킹) 다른 경로를 탐색함.
- PreOrder, InOrder, PostOrder이 전부 DFS의 한 종류 / 트리에서 기본으로 쓰이는 방법
public class DepthFirstSearch : MonoBehaviour
{
// 그래프를 인접 행렬(Adjacency Matrix) 방식로 표현 (8x8 행렬)
// nodes[i, j] == 1이면 i번 노드와 j번 노드가 서로 연결되어 있다
// <-> nodes[i, j] == 0이면 연결되어 있지 않다는 의미입니다.
private int[,] nodes = new int[8, 8]
{
// 0 1 2 3 4 5 6 7
{0, 1, 1, 1, 0, 0, 0, 0}, // 0번 노드의 연결 상태
{1, 0, 0, 0, 1, 1, 0, 0}, // 1번 노드
{1, 0, 0, 0, 0, 0, 0, 0}, // 2번 노드
{1, 0, 0, 0, 0, 0, 1, 0}, // 3번 노드
{0, 1, 0, 0, 0, 1, 0, 0}, // 4번 노드
{0, 1, 0, 0, 1, 0, 0, 1}, // 5번 노드
{0, 0, 0, 1, 0, 0, 0, 0}, // 6번 노드
{0, 0, 0, 0, 0, 1, 0, 0}, // 7번 노드
};
// 탐색할 노드들을 저장하는 스택 (후입선출 LIFO)
public Stack<int> stack = new Stack<int>();
private bool[] visited = new bool[8]; // 각 노드의 방문 여부를 기록하는 배열 (크기가 8) (중복방문방지)
void Start()
{
// 0번 노드부터 DFS 시작
DFSearch(0);
}
// 깊이 우선 탐색(DFS)
private void DFSearch(int start)
{
stack.Push(start); // 1. 시작 노드를 스택에 추가
while (stack.Count > 0) // 2. 스택이 비어있지 않은 동안 반복
{
// 3. 스택에서 가장 위에 있는 노드(index)를 꺼냄
int index = stack.Pop();
if (!visited[index]) // 4. 현재 노드(index)를 아직 방문하지 않았다면
{
// 5. 방문 표시 , 방문 순서를 콘솔에 출력
visited[index] = true;
Debug.Log($"{index}번 노드에 방문");
// 6. 현재 노드(index)와 연결된 모든 이웃 노드를 탐색
// (연결된 노드들을 7부터 0까지 역순으로 넣기 -> 그래야 차례로 나옴 LIFO)
for (int i = nodes.GetLength(0) - 1; i >= 0; i--)
{
// 연결되어 있고 아직 방문하지 않았다면 스택에 추가
if (nodes[index, i] == 1 && !visited[i])
stack.Push(i);
}
}
}
}
}
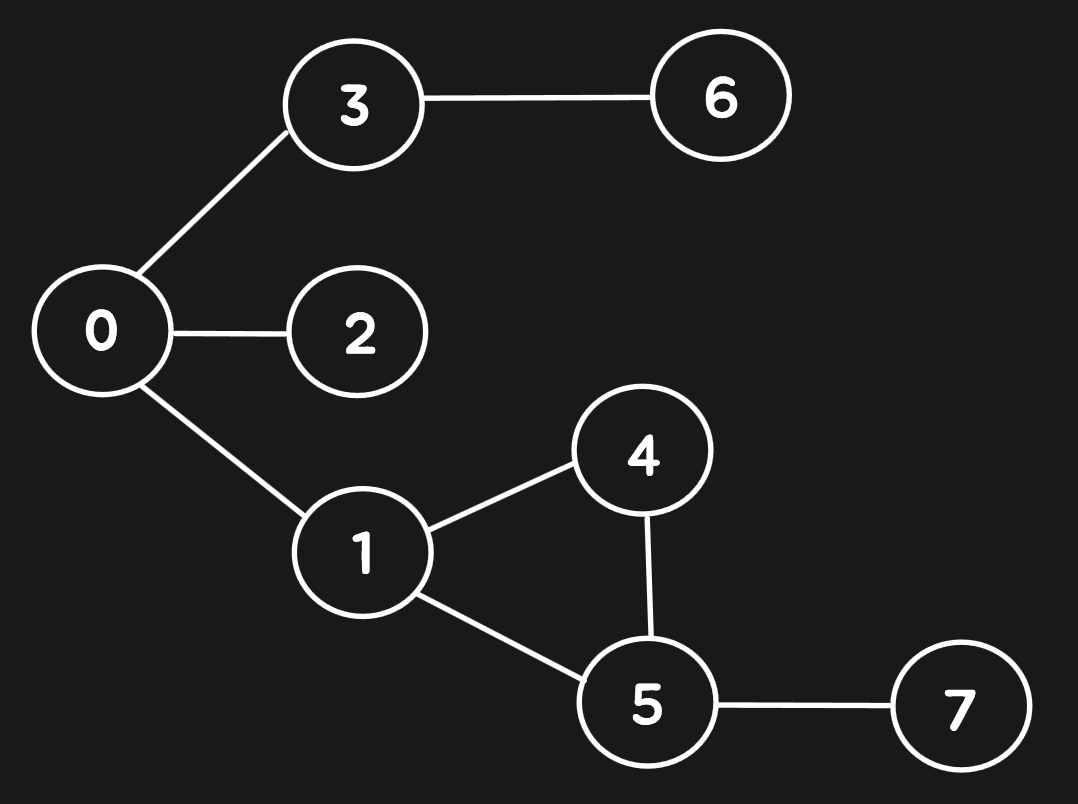
출력 결과
0번 노드에 방문
1번 노드에 방문
4번 노드에 방문
5번 노드에 방문
7번 노드에 방문
2번 노드에 방문
3번 노드에 방문
6번 노드에 방문
시작 노드: 0번
Start() 메서드 실행
void Start()가 호출되고, DFSearch(0)를 호출합니다.
DFSearch(int start) 메서드 실행 (start = 0)
초기 상태:
- stack (스택): 비어 있음 []
- visited (방문 배열): [F, F, F, F, F, F, F, F] (모두 false)
단계 1: stack.Push(start); (start = 0)
- 0번 노드를 스택에 넣습니다.
- stack: [0]
- visited: [F, F, F, F, F, F, F, F]
단계 2: while (stack.Count > 0) 루프 시작 (스택에 0이 있으므로 조건 참)
단계 2.1: int index = stack.Pop();
- 스택에서 0을 꺼냅니다.
- index = 0
- stack: []
단계 2.2: if (!visited[index]) (index = 0)
- !visited[0] (즉, !false) 이므로 조건 참. (0번 노드는 아직 방문하지 않았습니다.)
단계 2.3: visited[index] = true;
- visited[0]을 true로 설정합니다.
- visited: [T, F, F, F, F, F, F, F]
단계 2.4: Debug.Log($"{index}번 노드에 방문");
- 콘솔 출력: 0번 노드에 방문
단계 2.5: for (int i = nodes.GetLength(0) - 1; i >= 0; i--) 루프 시작 (i = 7부터 0까지)
- index (0번 노드)와 연결된 이웃 노드를 찾아서 스택에 넣습니다.
- nodes[0, i] == 1이고 !visited[i]인 경우 stack.Push(i)
- i = 7: nodes[0, 7]은 0. 조건 불만족.
- i = 6: nodes[0, 6]은 0. 조건 불만족.
- i = 5: nodes[0, 5]은 0. 조건 불만족.
- i = 4: nodes[0, 4]은 0. 조건 불만족.
- i = 3: nodes[0, 3]은 1. !visited[3] (즉, !false) 이므로 조건 만족.
- stack.Push(3)
- stack: [3]
- i = 2: nodes[0, 2]은 1. !visited[2] (즉, !false) 이므로 조건 만족.
- stack.Push(2)
- stack: [3, 2]
- i = 1: nodes[0, 1]은 1. !visited[1] (즉, !false) 이므로 조건 만족.
- stack.Push(1)
- stack: [3, 2, 1] (스택의 맨 위는 1)
- i = 0: nodes[0, 0]은 0. 조건 불만족.
단계 3: while (stack.Count > 0) 루프 재시작 (스택에 1, 2, 3이 있으므로 조건 참)
단계 3.1: int index = stack.Pop();
- 스택에서 1을 꺼냅니다. (스택은 LIFO이므로 가장 최근에 들어간 1이 먼저 나옵니다.)
- index = 1
- stack: [3, 2]
단계 3.2: if (!visited[index]) (index = 1)
- !visited[1] (즉, !false) 이므로 조건 참. (1번 노드는 아직 방문하지 않았습니다.)
단계 3.3: visited[index] = true;
- visited[1]을 true로 설정합니다.
- visited: [T, T, F, F, F, F, F, F]
단계 3.4: Debug.Log($"{index}번 노드에 방문");
- 콘솔 출력: 1번 노드에 방문
단계 3.5: for (int i = nodes.GetLength(0) - 1; i >= 0; i--) 루프 시작 (i = 7부터 0까지)
- index (1번 노드)와 연결된 이웃 노드를 찾아서 스택에 넣습니다.
- nodes[1, i] == 1이고 !visited[i]인 경우 stack.Push(i)
- i = 7: nodes[1, 7]은 0. 조건 불만족.
- i = 6: nodes[1, 6]은 0. 조건 불만족.
- i = 5: nodes[1, 5]은 1. !visited[5] (즉, !false) 이므로 조건 만족.
- stack.Push(5)
- stack: [3, 2, 5]
- i = 4: nodes[1, 4]은 1. !visited[4] (즉, !false) 이므로 조건 만족.
- stack.Push(4)
- stack: [3, 2, 5, 4]
- i = 3: nodes[1, 3]은 0. 조건 불만족.
- i = 2: nodes[1, 2]은 0. 조건 불만족.
- i = 1: nodes[1, 1]은 0. 조건 불만족.
- i = 0: nodes[1, 0]은 1. !visited[0] (즉, !true) 이므로 조건 불만족. (0번은 이미 방문했으므로 스택에 넣지 않습니다.)
단계 4: while (stack.Count > 0) 루프 재시작 (스택에 2, 3, 4, 5가 있으므로 조건 참)
단계 4.1: int index = stack.Pop();
- 스택에서 4를 꺼냅니다.
- index = 4
- stack: [3, 2, 5]
단계 4.2: if (!visited[index]) (index = 4)
- !visited[4] (즉, !false) 이므로 조건 참. (4번 노드는 아직 방문하지 않았습니다.)
단계 4.3: visited[index] = true;
- visited[4]을 true로 설정합니다.
- visited: [T, T, F, F, T, F, F, F]
단계 4.4: Debug.Log($"{index}번 노드에 방문");
- 콘솔 출력: 4번 노드에 방문
단계 4.5: for (int i = nodes.GetLength(0) - 1; i >= 0; i--) 루프 시작 (i = 7부터 0까지)
- index (4번 노드)와 연결된 이웃 노드를 찾아서 스택에 넣습니다.
- nodes[4, i] == 1이고 !visited[i]인 경우 stack.Push(i)
- i = 7: nodes[4, 7]은 0. 조건 불만족.
- i = 6: nodes[4, 6]은 0. 조건 불만족.
- i = 5: nodes[4, 5]은 1. !visited[5] (즉, !false) 이므로 조건 만족.
- stack.Push(5)
- stack: [3, 2, 5, 5]
- i = 4: nodes[4, 4]은 0. 조건 불만족.
- i = 3: nodes[4, 3]은 0. 조건 불만족.
- i = 2: nodes[4, 2]은 0. 조건 불만족.
- i = 1: nodes[4, 1]은 1. !visited[1] (즉, !true) 이므로 조건 불만족.
- i = 0: nodes[4, 0]은 0. 조건 불만족.
단계 5: while (stack.Count > 0) 루프 재시작 (스택에 2, 3, 5, 5가 있으므로 조건 참)
단계 5.1: int index = stack.Pop();
- 스택에서 5를 꺼냅니다.
- index = 5
- stack: [3, 2, 5]
단계 5.2: if (!visited[index]) (index = 5)
- !visited[5] (즉, !false) 이므로 조건 참. (5번 노드는 아직 방문하지 않았습니다.)
단계 5.3: visited[index] = true;
- visited[5]을 true로 설정합니다.
- visited: [T, T, F, F, T, T, F, F]
단계 5.4: Debug.Log($"{index}번 노드에 방문");
- 콘솔 출력: 5번 노드에 방문
단계 5.5: for (int i = nodes.GetLength(0) - 1; i >= 0; i--) 루프 시작 (i = 7부터 0까지)
- index (5번 노드)와 연결된 이웃 노드를 찾아서 스택에 넣습니다.
- nodes[5, i] == 1이고 !visited[i]인 경우 stack.Push(i)
- i = 7: nodes[5, 7]은 1. !visited[7] (즉, !false) 이므로 조건 만족.
- stack.Push(7)
- stack: [3, 2, 5, 7]
- i = 6: nodes[5, 6]은 0. 조건 불만족.
- i = 5: nodes[5, 5]은 0. 조건 불만족.
- i = 4: nodes[5, 4]은 1. !visited[4] (즉, !true) 이므로 조건 불만족.
- i = 3: nodes[5, 3]은 0. 조건 불만족.
- i = 2: nodes[5, 2]은 0. 조건 불만족.
- i = 1: nodes[5, 1]은 1. !visited[1] (즉, !true) 이므로 조건 불만족.
- i = 0: nodes[5, 0]은 0. 조건 불만족.
- i = 7: nodes[5, 7]은 1. !visited[7] (즉, !false) 이므로 조건 만족.
단계 6: while (stack.Count > 0) 루프 재시작 (스택에 2, 3, 5, 7이 있으므로 조건 참)
단계 6.1: int index = stack.Pop();
- 스택에서 7을 꺼냅니다.
- index = 7
- stack: [3, 2, 5]
단계 6.2: if (!visited[index]) (index = 7)
- !visited[7] (즉, !false) 이므로 조건 참. (7번 노드는 아직 방문하지 않았습니다.)
단계 6.3: visited[index] = true;
- visited[7]을 true로 설정합니다.
- visited: [T, T, F, F, T, T, F, T]
단계 6.4: Debug.Log($"{index}번 노드에 방문");
- 콘솔 출력: 7번 노드에 방문
단계 6.5: for (int i = nodes.GetLength(0) - 1; i >= 0; i--) 루프 시작 (i = 7부터 0까지)
- index (7번 노드)와 연결된 이웃 노드를 찾아서 스택에 넣습니다.
- nodes[7, i] == 1이고 !visited[i]인 경우 stack.Push(i)
- i = 7: nodes[7, 7]은 0. 조건 불만족.
- i = 6: nodes[7, 6]은 0. 조건 불만족.
- i = 5: nodes[7, 5]은 1. !visited[5] (즉, !true) 이므로 조건 불만족.
- 나머지 i 값들도 nodes[7, i]가 0이거나 이미 방문한 노드이므로 조건 불만족.
단계 7: while (stack.Count > 0) 루프 재시작 (스택에 2, 3, 5가 있으므로 조건 참)
단계 7.1: int index = stack.Pop();
- 스택에서 5를 꺼냅니다.
- index = 5
- stack: [3, 2]
단계 7.2: if (!visited[index]) (index = 5)
- !visited[5] (즉, !true) 이므로 조건 거짓. (5번 노드는 이미 방문했습니다.)
- 따라서 이 노드에 대한 방문 처리(Debug.Log 등) 및 이웃 노드 탐색은 건너뜁니다.
단계 8: while (stack.Count > 0) 루프 재시작 (스택에 2, 3이 있으므로 조건 참)
단계 8.1: int index = stack.Pop();
- 스택에서 2를 꺼냅니다.
- index = 2
- stack: [3]
단계 8.2: if (!visited[index]) (index = 2)
- !visited[2] (즉, !false) 이므로 조건 참. (2번 노드는 아직 방문하지 않았습니다.)
단계 8.3: visited[index] = true;
- visited[2]을 true로 설정합니다.
- visited: [T, T, T, F, T, T, F, T]
단계 8.4: Debug.Log($"{index}번 노드에 방문");
- 콘솔 출력: 2번 노드에 방문
단계 8.5: for (int i = nodes.GetLength(0) - 1; i >= 0; i--) 루프 시작 (i = 7부터 0까지)
- index (2번 노드)와 연결된 이웃 노드를 찾아서 스택에 넣습니다.
- nodes[2, i] == 1이고 !visited[i]인 경우 stack.Push(i)
- i = 0: nodes[2, 0]은 1. !visited[0] (즉, !true) 이므로 조건 불만족.
- 나머지 i 값들도 nodes[2, i]가 0이므로 조건 불만족.
단계 9: while (stack.Count > 0) 루프 재시작 (스택에 3이 있으므로 조건 참)
단계 9.1: int index = stack.Pop();
- 스택에서 3을 꺼냅니다.
- index = 3
- stack: []
단계 9.2: if (!visited[index]) (index = 3)
- !visited[3] (즉, !false) 이므로 조건 참. (3번 노드는 아직 방문하지 않았습니다.)
단계 9.3: visited[index] = true;
- visited[3]을 true로 설정합니다.
- visited: [T, T, T, T, T, T, F, T]
단계 9.4: Debug.Log($"{index}번 노드에 방문");
- 콘솔 출력: 3번 노드에 방문
단계 9.5: for (int i = nodes.GetLength(0) - 1; i >= 0; i--) 루프 시작 (i = 7부터 0까지)
- index (3번 노드)와 연결된 이웃 노드를 찾아서 스택에 넣습니다.
- nodes[3, i] == 1이고 !visited[i]인 경우 stack.Push(i)
- i = 6: nodes[3, 6]은 1. !visited[6] (즉, !false) 이므로 조건 만족.
- stack.Push(6)
- stack: [6]
- i = 0: nodes[3, 0]은 1. !visited[0] (즉, !true) 이므로 조건 불만족.
- 나머지 i 값들은 nodes[3, i]가 0이므로 조건 불만족.
- i = 6: nodes[3, 6]은 1. !visited[6] (즉, !false) 이므로 조건 만족.
단계 10: while (stack.Count > 0) 루프 재시작 (스택에 6이 있으므로 조건 참)
단계 10.1: int index = stack.Pop();
- 스택에서 6을 꺼냅니다.
- index = 6
- stack: []
단계 10.2: if (!visited[index]) (index = 6)
- !visited[6] (즉, !false) 이므로 조건 참. (6번 노드는 아직 방문하지 않았습니다.)
단계 10.3: visited[index] = true;
- visited[6]을 true로 설정합니다.
- visited: [T, T, T, T, T, T, T, T]
단계 10.4: Debug.Log($"{index}번 노드에 방문");
- 콘솔 출력: 6번 노드에 방문
단계 10.5: for (int i = nodes.GetLength(0) - 1; i >= 0; i--) 루프 시작 (i = 7부터 0까지)
- index (6번 노드)와 연결된 이웃 노드를 찾아서 스택에 넣습니다.
- nodes[6, i] == 1이고 !visited[i]인 경우 stack.Push(i)
- i = 3: nodes[6, 3]은 1. !visited[3] (즉, !true) 이므로 조건 불만족.
- 나머지 i 값들은 nodes[6, i]가 0이므로 조건 불만족.
단계 11: while (stack.Count > 0) 루프 재시작 (스택이 비어 있으므로 조건 거짓)
- 루프가 종료됩니다.
- DFSearch 함수가 종료됩니다.
최종 콘솔 출력 순서
위의 과정을 통해 Unity 콘솔에 출력되는 메시지 순서는 다음과 같습니다.
- 0번 노드에 방문
- 1번 노드에 방문
- 4번 노드에 방문
- 5번 노드에 방문
- 7번 노드에 방문
- 2번 노드에 방문
- 3번 노드에 방문
- 6번 노드에 방문
6. 너비 우선 탐색 (BFS : Breadth First Search)
: 같은 깊이의 노드부터 차례로 탐색하는 알고리즘
(시작 노드에서부터 가까운 노드들을 먼저 모두 탐색하고, 그 다음으로 가까운 노드들을 탐색하는 식으로 진행)
public class BreadthFirstSearch : MonoBehaviour
{
private int[,] nodes = new int[8, 8]
{
// 0 1 2 3 4 5 6 7
{0, 1, 1, 1, 0, 0, 0, 0}, // 0번 노드
{1, 0, 0, 0, 1, 1, 0, 0}, // 1번 노드
{1, 0, 0, 0, 0, 0, 0, 0}, // 2번 노드
{1, 0, 0, 0, 0, 0, 1, 0}, // 3번 노드
{0, 1, 0, 0, 0, 1, 0, 0}, // 4번 노드
{0, 1, 0, 0, 1, 0, 0, 1}, // 5번 노드
{0, 0, 0, 1, 0, 0, 0, 0}, // 6번 노드
{0, 0, 0, 0, 0, 1, 0, 0}, // 7번 노드
};
// BFS 탐색에 사용할 큐 (선입선출 FIFO)
public Queue<int> queue = new Queue<int>();
private bool[] visited = new bool[8];
void Start()
{
BFSearch(0); // 0번 노드에서 BFS 시작
}
// 너비 우선 탐색(BFS)
private void BFSearch(int start)
{
queue.Enqueue(start); // 1. 시작 노드를 큐에 넣고 탐색 시작
while (queue.Count > 0) // 2. 큐가 비어있지 않은 동안 반복
{
int index = queue.Dequeue(); //// 3. 큐에서 가장 먼저 들어온 노드(index)를 꺼냄
if (!visited[index]) // 4. 현재 노드(index)를 아직 방문하지 않았다면
{
visited[index] = true; // 5. 방문 처리 , 콘솔에 출력
Debug.Log($"{index}번 노드에 방문");
// 6. 현재 노드(index)와 연결된 모든 이웃 노드를 탐색
// DFS 코드와 달리 for 루프가 0부터 nodes.GetLength(0) - 1까지 순방향으로
for (int i = 0; i < nodes.GetLength(0); i++)
{
// 연결되어 있고 아직 방문하지 않았다면 큐에 추가
if (nodes[index, i] == 1 && !visited[i])
queue.Enqueue(i);
}
}
}
}
}
- BFSearch(0) 호출, queue.Enqueue(0)
- 큐: [0]
- 큐에서 0 Dequeue. visited[0] = true. "0번 노드 방문".
- 0번과 연결된 노드: 1, 2, 3 (순방향으로 큐에 넣음)
- queue.Enqueue(1)
- queue.Enqueue(2)
- queue.Enqueue(3)
- 큐: [1, 2, 3]
- 큐에서 1 Dequeue. visited[1] = true. "1번 노드 방문".
- 1번과 연결된 노드: 0, 4, 5 (0번은 이미 방문했으므로 무시)
- queue.Enqueue(4)
- queue.Enqueue(5)
- 큐: [2, 3, 4, 5]
- 큐에서 2 Dequeue. visited[2] = true. "2번 노드 방문".
- 2번과 연결된 노드: 0 (0번은 이미 방문했으므로 무시)
- 큐: [3, 4, 5]
- 큐에서 3 Dequeue. visited[3] = true. "3번 노드 방문".
- 3번과 연결된 노드: 0, 6 (0번은 이미 방문했으므로 무시)
- queue.Enqueue(6)
- 큐: [4, 5, 6]
- 큐에서 4 Dequeue. visited[4] = true. "4번 노드 방문".
- 4번과 연결된 노드: 1, 5 (1번은 방문, 5번은 이미 큐에 있지만 아직 방문X)
- 중요: 이 코드에서는 큐에 넣기 전에 !visited[i]를 체크하므로, 5번은 이미 큐에 있지만 다시 들어가지 않습니다. if (nodes[index, i] == 1 && !visited[i]) 조건 때문입니다.
- 큐: [5, 6]
- 4번과 연결된 노드: 1, 5 (1번은 방문, 5번은 이미 큐에 있지만 아직 방문X)
- 큐에서 5 Dequeue. visited[5] = true. "5번 노드 방문".
- 5번과 연결된 노드: 1, 4, 7 (1, 4번은 방문)
- queue.Enqueue(7)
- 큐: [6, 7]
- 큐에서 6 Dequeue. visited[6] = true. "6번 노드 방문".
- 6번과 연결된 노드: 3 (3번은 방문)
- 큐: [7]
- 큐에서 7 Dequeue. visited[7] = true. "7번 노드 방문".
- 7번과 연결된 노드: 5 (5번은 방문)
- 큐: []
- 큐가 비었으므로 루프 종료.
//출력순서 - 가까운 순
0번 노드에 방문
1번 노드에 방문
2번 노드에 방문
3번 노드에 방문
4번 노드에 방문
5번 노드에 방문
6번 노드에 방문
7번 노드에 방문
| DFS (Depth-First Search) | BFS (Breadth-First Search) | |
| 탐색 방식 | 깊이 우선: 한 경로로 끝까지 탐색 | 너비 우선: 가까운 노드부터 탐색 |
| 자료구조 | 스택(Stack) (혹은 재귀 호출) | 큐(Queue) |
| 방문 순서 | 깊이 → 되돌아옴(백트래킹) | 레벨 순서(거리 순)로 방문 |
| 최단 경로 보장 | 보장 안 됨 | 보장됨 |
| 공간 복잡도 | O(노드 수) (최악의 경우 트리 높이만큼 스택 사용) | O(노드 수) (최대 노드 수만큼 큐 필요) |
| 적합한 경우 | 경로의 깊이가 중요한 경우 (예: 미로 찾기) | 최단 경로가 중요한 경우 |
| 구현 난이도 | 상대적으로 간단 (재귀 활용) | 큐를 써야 해서 구조적 |
| 예시 사용 | 미로 탐색, 퍼즐 문제 | 최단 거리 문제, 친구 추천, GPS |
'프로그래밍 > 유니티 부트캠프' 카테고리의 다른 글
| 유니티 교재 정리 (96pg~ 247pg) 멋쟁이사자처럼 41,42회차 (1) | 2025.07.24 |
|---|---|
| 유니티(다익스트라 알고리즘, 정렬 - 선택 정렬, 삽입 정렬, 버블 정렬, 퀵 정렬) _ 멋쟁이사자처럼 유니티 부트캠프 후기 40회차 (1) | 2025.07.14 |
| 유니티(하노이의 탑 2,UI Stack, Queue 오브젝트 풀, 알고리즘1) _ 멋쟁이사자처럼 유니티 부트캠프 후기 38회차 (6) | 2025.07.10 |
| 유니티(리스트, 스택 실습 _ 하노이의 탑) _ 멋쟁이사자처럼 유니티 부트캠프 후기 37회차 (0) | 2025.07.10 |
| 유니티(자료구조2, 형상관리 깃브랜치, 배열 예제_3D_폭탄) _ 멋쟁이사자처럼 유니티 부트캠프 후기 36회차 (0) | 2025.07.08 |
